Just reading around and stumble upon the decent espresso machine being built. Sounds like it ticks all the boxes. Anyone heard any more about it??

2,921 - 2,940 of 4,197 Posts
Joined
·
558 Posts
@decent_espresso Is there anywhere on the website that shows the prices of the previous generation of machines and the various options on those (cosmetic seconds, used machines etc)
Joined
·
2,027 Posts
Here you can see the price difference between v1.1 and v1.3: https://decentespresso.com/model@decent_espresso Is there anywhere on the website that shows the prices of the previous generation of machines and the various options on those (cosmetic seconds, used machines etc)
Only feature difference is the group head controller, added to v1.3.
Price discount scheme for used/cosmetic seconds is here below on the instagram page but FYI not a single owner has traded in their old DE1 for a newer model, so there are no used models for sale, nor likely to be very many.
We do have a few (~10) very lightly mirror-panel-scratched v1.1 models at 10% off (one scratch, and under 1cm in length), and if you'd like to know about those, please write to us at http://decentespresso.com/contact
https://www.coffeeforums.co.uk/index.php?app=core&module=system&controller=embed&url=https://www.instagram.com/p/B8eX_RdBnoj/
Joined
·
1,525 Posts
Obviously I'm only wasting my own time, but I look at the queue from time to time and my order has moved down the queue twice. Hopefully all it means is I'll get it, say, 17th May rather than 16th May!
Joined
·
615 Posts
A good month May?Obviously I'm only wasting my own time, but I look at the queue from time to time and my order has moved down the queue twice. Hopefully all it means is I'll get it, say, 17th May rather than 16th May!
Joined
·
2,027 Posts
Coronavirus is messing things up, apologies for that. UPS suspended shipments for 10 days, now they're asking us to use another courier to get things to their warehouse. Things are not normal at the moment.Obviously I'm only wasting my own time, but I look at the queue from time to time and my order has moved down the queue twice. Hopefully all it means is I'll get it, say, 17th May rather than 16th May!
I'm just about to leave New York City, which apparently is about to go into "lockdown" with everyone confined to their home, like in San Francisco, where I'm flying to.
-john
Joined
·
1,525 Posts
No apologies needed, John. I was just making a remark for the sake of making a remark - no criticism intended. I did receive my v2 tamper today, though. Hefty!Coronavirus is messing things up, apologies for that. UPS suspended shipments for 10 days, now they're asking us to use another courier to get things to their warehouse. Things are not normal at the moment.
I'm just about to leave New York City, which apparently is about to go into "lockdown" with everyone confined to their home, like in San Francisco, where I'm flying to.
-john
Joined
·
2,027 Posts

Trouble shipping out
A few people have noticed that our order queue https://decentespresso.com/queue hasn't been moving lately.
The reason: we've had troubles getting espresso machines shipped for the past 10 days. UPS initially refused our orders, then refused to pick up and told us to use another courrier to get packages inside Hong Kong, to the UPS warehouse. Strange.
And today...
We learned about UPS rules in effect: a limit of 150kg of packages shipped per day to the USA, and 300kg per day to EU. That's 6 machines to the USA per day, 12 to EU. That's why they were being weird to us and not accepting all our shipments, and it seems arbitrary. We can work around this limitation now that we know what it is. We are now shipping directly, using our own UPS account, instead of our usual shipping broker.
We're pretty sure that our shipping broker had gone over their limit, and that's why we have been mostly blocked from shipping for the past 10 days.
Unfortunately, they weren't communicative, and didn't tell us that this was the issue. Probably they didn't want us to bypass them, which we needed to do, to get around the daily limit that was imposed on them.
We are now shipping machines directly from our our UPS account, and not using the broker, in order to bypass these limits. It's a bit more expensive for us, but we "gotta do what we gotta do". We're swallowing the extra shipping cost (using the broker is cheaper) and not asking customers for more shipping money.
I'm fairly sure that these quotas are due to Hong Kong being the world's largest air freight airport. With China's factories back in operation, the coronavirus-struck world needs stuff, badly, and logistics companies are straining under the load. UPS is trying to be fair and evenly spread the load.
-john
Attachments
-
63.9 KB Views: 21
Joined
·
2,027 Posts
The "shower basket" is coming
In about two weeks, we should have the pour over "shower baskets" in stock, and will ship them to everyone who has back ordered one. https://decentespresso.com/basket
To prepare for this, I'm currently working on:
- getting several new profiles from Scott Rao, for different "pour over" recipes, using the new shower basket, for different grind dose weights.
- a video from Rao showing how to make this new kind of pour-over: https://youtu.be/HraNBzMaCW8
- a new feature to hide profiles you don't want to see. It's an eyeball icon, and then you uncheck the profiles you want to hide.
![]()
- We're trying to find a water resistant "motorized cake display stand" to sit the V60 on, so that you don't have to do a stir, and the possibility of channeling is further reduced. For example https://www.amazon.com/gp/product/B01M5HN2AU/ (but able to handle water pouring on it). If you have any tips, please let me know. Rao found he got another 1% extraction when using a (non-water-resistant) rotating stand under his v60.
![]()
In about two weeks, we should have the pour over "shower baskets" in stock, and will ship them to everyone who has back ordered one. https://decentespresso.com/basket
To prepare for this, I'm currently working on:
- getting several new profiles from Scott Rao, for different "pour over" recipes, using the new shower basket, for different grind dose weights.
- a video from Rao showing how to make this new kind of pour-over: https://youtu.be/HraNBzMaCW8
- a new feature to hide profiles you don't want to see. It's an eyeball icon, and then you uncheck the profiles you want to hide.
- We're trying to find a water resistant "motorized cake display stand" to sit the V60 on, so that you don't have to do a stir, and the possibility of channeling is further reduced. For example https://www.amazon.com/gp/product/B01M5HN2AU/ (but able to handle water pouring on it). If you have any tips, please let me know. Rao found he got another 1% extraction when using a (non-water-resistant) rotating stand under his v60.

Attachments
-
66.6 KB Views: 85
-
652.2 KB Views: 96
Joined
·
2,027 Posts
New feature: How to show and hide presets
By default, only the most popular espresso presets are shown on the Decent Espresso machine. You can choose to show more, or hide those you do not want. Any preset you create, is shown by default.
I've sometimes found myself struggling to find the preset I wan, mixed in the long list. I'm hoping this new feature addresses that problem.
Joined
·
2,027 Posts
New: puck resistance
A new feature today in the Decent App, suggested by Collin Arneson in long conversation about "Stalled Extractions" (itself an interesting topic) brings "Puck resistance" to the Decent Espresso App.
This new feature appears as a chart line, giving you an idea of how well your puck is resisting water flow.
Another way to think of this new line, is as a representation of your "coffee puck integrity".
"Puck resistance" should usually go down over time, since about 20% of the puck material ends up in your espresso. Less puck material should mean less puck resistance to water.
Because it is calculated as "pressure/flow", it allows you to see the quality of the puck, somewhat independently of a changing pressure or changing flow rate. There are no objective "units" to this: this is a "made up" calculated number that seemed useful in conversation.
Note that this line is only (at the moment) in the "Insight" skin, and only when you tap to zoom the chart. The new line is in Yellow, as its label.
-john
Attachments
-
128.7 KB Views: 18
Joined
·
2,027 Posts
Puck resistance : revisited
Yesterday I added "puck resistance" to Decent the App, calculated as "pressure / flow"
But, this calculation bothered me, and it took me a day to figure out why.
Those of us who have made flow profiled shots have noticed that a small chance in flow, yields a big difference in pressure. Yes, the "resistance" calculation we were using yesterday, implies a linear relationship.
I've heard Ray tell me that pressure increases to the square of flow. Hopefully I didn't misunderstand. I went searching online for more about this, and that seems to be the case, but "I am not a physicist" so please... someone correct me.
I have now changed the "puck resistance" calculation to be: pressure / (flow^2) and I'm so far, happier with the results the resistance line is giving me, which are now closer to what I think is actually going on.
In 3 espressos, let me explain.My first espresso was at Niche's grind setting 11, and the flow was a touch too fast, and the shot ended a bit too soon. Puck resistance never amounted to much:
![]()
So, I tried grinding 1 notch finer.My second espresso was at Niche's grind setting 10 (finer), with 17g of coffee, 36g in cup (39ml using volumetric stopping). The espresso starts with just a few drips, and "puck resistance" goes "off the chart" to represent this almost "stuck puck" that is the start of my espresso shot. The shot took a long time to finish, and was still fairly slow at the end.
![]()
Instead of changing the grind, I reduced my dose by 1.5g, and I got a shot that had almost linear puck resistance dropping, and flat flow. The slight pressure drop around 23 seconds kept flow constant as puck resistance dropped slightly. But very little pressure adjustment was needed, as puck resistance was holding well.
![]()
If pressure is held constant, then the flow gives you a reasonable idea of puck resistance. That's what Matt Perger is doing with his DE1, to test his distribution tool. Here is an unpublished photo of one of his tests. Notice how he's using 9 bar constant, in order to assess how well his grooming tool is working at maintaining puck integrity.
![]()
Once Matt gets back to his DE1, after the coronavirus lockdown, he'll be able to vary pressure, and now, assess puck resistance as an independent variable.
Interesting times.
-john
Yesterday I added "puck resistance" to Decent the App, calculated as "pressure / flow"
But, this calculation bothered me, and it took me a day to figure out why.
Those of us who have made flow profiled shots have noticed that a small chance in flow, yields a big difference in pressure. Yes, the "resistance" calculation we were using yesterday, implies a linear relationship.
I've heard Ray tell me that pressure increases to the square of flow. Hopefully I didn't misunderstand. I went searching online for more about this, and that seems to be the case, but "I am not a physicist" so please... someone correct me.
I have now changed the "puck resistance" calculation to be: pressure / (flow^2) and I'm so far, happier with the results the resistance line is giving me, which are now closer to what I think is actually going on.
In 3 espressos, let me explain.My first espresso was at Niche's grind setting 11, and the flow was a touch too fast, and the shot ended a bit too soon. Puck resistance never amounted to much:

So, I tried grinding 1 notch finer.My second espresso was at Niche's grind setting 10 (finer), with 17g of coffee, 36g in cup (39ml using volumetric stopping). The espresso starts with just a few drips, and "puck resistance" goes "off the chart" to represent this almost "stuck puck" that is the start of my espresso shot. The shot took a long time to finish, and was still fairly slow at the end.

Instead of changing the grind, I reduced my dose by 1.5g, and I got a shot that had almost linear puck resistance dropping, and flat flow. The slight pressure drop around 23 seconds kept flow constant as puck resistance dropped slightly. But very little pressure adjustment was needed, as puck resistance was holding well.

If pressure is held constant, then the flow gives you a reasonable idea of puck resistance. That's what Matt Perger is doing with his DE1, to test his distribution tool. Here is an unpublished photo of one of his tests. Notice how he's using 9 bar constant, in order to assess how well his grooming tool is working at maintaining puck integrity.
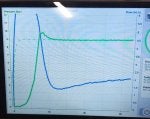
Once Matt gets back to his DE1, after the coronavirus lockdown, he'll be able to vary pressure, and now, assess puck resistance as an independent variable.
Interesting times.
-john
Attachments
-
298 KB Views: 18
-
321.6 KB Views: 28
-
311.3 KB Views: 15
-
80.8 KB Views: 15
John, your calculation is correct. If you use m3/hr for the flow and bars for the pressure then you are actually calculating the Kv value of the puck (plus that of the basket and any other resistance to flow you may have in the system if you are pedantic).
Most interesting the way the resistance builds up as the puck saturates.
Concerning your precision baskets, have you considered measuring the Kv values of these in comparison to standard baskets. It has to be this which is the real differentiator between them, rather than improvements in precision.
Most interesting the way the resistance builds up as the puck saturates.
Concerning your precision baskets, have you considered measuring the Kv values of these in comparison to standard baskets. It has to be this which is the real differentiator between them, rather than improvements in precision.
Joined
·
2,027 Posts
I'm not sure Kv would be a useful scale, as a square meter of water is a LOT more than espresso would likely ever use. We're in the range of 2 ml/s, which is 7200 ml/hour, or 7.2 liters per hour.John, your calculation is correct. If you use m3/hr for the flow and bars for the pressure then you are actually calculating the Kv value of the puck
But it's nice that I'm at least using a scale version of a real value.
Do you mean, Kv without any coffee in them? I do make the drawings and hole sizes available, for each basket we make, if you're curious.Concerning your precision baskets, have you considered measuring the Kv values of these in comparison to standard baskets. It has to be this which is the real differentiator between them, rather than improvements in precision.
I do think precision of the hole, though, is a big factor, at least as far as even-ness of the area punched through. I've looked at £2 baskets under a microscope, and their holes are both non-circular, and widely varying in size.
You are absolutely right that to display it as a true Kv would not be useful - what you are displaying is Kv *1000, which is better.
I did mean the Kv of the baskets without any coffee. If you have the right rig it would be simple enough to measure but I do not think it can be modelled with any accuracy. I just think it might be interesting to know the significance of the basket resistance to that of the puck.
I did mean the Kv of the baskets without any coffee. If you have the right rig it would be simple enough to measure but I do not think it can be modelled with any accuracy. I just think it might be interesting to know the significance of the basket resistance to that of the puck.
Joined
·
2,027 Posts
Is there measurement name for that? "milliKv" ?You are absolutely right that to display it as a true Kv would not be useful - what you are displaying is Kv *1000, which is better.
Ah, I get it, that would be useful. We're currently measuring light passing through as a quality control test, using software John Weiss wrote for us. Similar idea.I did mean the Kv of the baskets without any coffee. If you have the right rig it would be simple enough to measure but I do not think it can be modelled with any accuracy. I just think it might be interesting to know the significance of the basket resistance to that of the puck.
-john
I have never heard of milli Kv, but why not.
Actually, I misled you a little, it is a late Friday night here. The correct definition of Kv is the other way round to what you are doing, i.e. Kv = flow/ sqrt(dP). Your calculation is also indicative of resistance but the indication is in opposite direction to Kv, i.e. at constant P, Kv increases with increasing flow, your indicator decreases.
Actually, I misled you a little, it is a late Friday night here. The correct definition of Kv is the other way round to what you are doing, i.e. Kv = flow/ sqrt(dP). Your calculation is also indicative of resistance but the indication is in opposite direction to Kv, i.e. at constant P, Kv increases with increasing flow, your indicator decreases.
Joined
·
2,027 Posts
Ah gotcha, reverse direction of the line, but perhaps easier to read in this context.I have never heard of milli Kv, but why not.
Actually, I misled you a little, it is a late Friday night here. The correct definition of Kv is the other way round to what you are doing, i.e. Kv = flow/ sqrt(dP). Your calculation is also indicative of resistance but the indication is in opposite direction to Kv, i.e. at constant P, Kv increases with increasing flow, your indicator decreases.
However: Jonathan Gagné is arguing elsewhere that this formula of mine is appropriate for turbulent flow, but that espresso is mostly laminar flow, and so this formula is not appropriate in our use case.
-john
Joined
·
2,027 Posts

Raoul's master class on the Decent Espresso machine went on, despite the coronavirus, now remotely! Here he is with Ahmed Nazmi of the Cairo Coffee Collective.
See more photos at:
The Institute for Coffee Excellence in Manilla, continues to do great work with Chief Caffeinator Raoul de Peralta and National Barista Champion (the Boss) Michael Harris Conlin .
-john
Attachments
-
200.5 KB Views: 19
Joined
·
2,027 Posts
Based on Gagné's advice, I had gone back to resistance=pressure/flow, but this did not give us lines that remain flat when a "puck simulator" basket was used. That's a blind basket with a hole punched in it. If the Resistance calculation were correct, it would stay constant despite changing flow or pressure.I have never heard of milli Kv, but why not.
Actually, I misled you a little, it is a late Friday night here. The correct definition of Kv is the other way round to what you are doing, i.e. Kv = flow/ sqrt(dP). Your calculation is also indicative of resistance but the indication is in opposite direction to Kv, i.e. at constant P, Kv increases with increasing flow, your indicator decreases.
Damian, author of the DSV skin https://www.diy.brakel.com.au/dsx/ has run with this problem, and his final formula is currently:
It is basically R = P/F^2, with some offset, scaling and alignment to fit the screen
It looks like this
y = Resistance
$a = Pressure
$c = Flow rate
set y [expr {(((($a+0.00001) / ((($c+0.0001)*($c+0.0001))+($a*0.9))) - 2)*5)+11}]
I think the .00001 stuff is him worrying too much about floating point math, but otherwise, his resuls is impressive, with constant resistance across lots of flow/pressure changes:

Attachments
-
42.8 KB Views: 30
The resistance expression is derived from the affinity laws so good to see that practice follows theory.Based on Gagné's advice, I had gone back to resistance=pressure/flow, but this did not give us lines that remain flat when a "puck simulator" basket was used. That's a blind basket with a hole punched in it. If the Resistance calculation were correct, it would stay constant despite changing flow or pressure.
Damian, author of the DSV skin https://www.diy.brakel.com.au/dsx/ has run with this problem, and his final formula is currently:
It is basically R = P/F^2, with some offset, scaling and alignment to fit the screen
It looks like this
y = Resistance
$a = Pressure
$c = Flow rate
set y [expr {(((($a+0.00001) / ((($c+0.0001)*($c+0.0001))+($a*0.9))) - 2)*5)+11}]
I think the .00001 stuff is him worrying too much about floating point math, but otherwise, his resuls is impressive, with constant resistance across lots of flow/pressure changes:
View attachment 37515
Is the 0.0001 term on the denominator there to avoid the possibility of dividing by zero?
2,921 - 2,940 of 4,197 Posts
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
-
?
- posts
- 904K
- members
- 44K
- Since
- 2008
A forum community dedicated to coffee enthusiasts. Come join the discussion about collections, retailers, beans, grinders, brewers, technical maintenance, models, styles, teas, reviews, accessories, classifieds, and more!
Explore Our Forums





